Вывод правила 7-10 для радиоактивности

[vashu11]

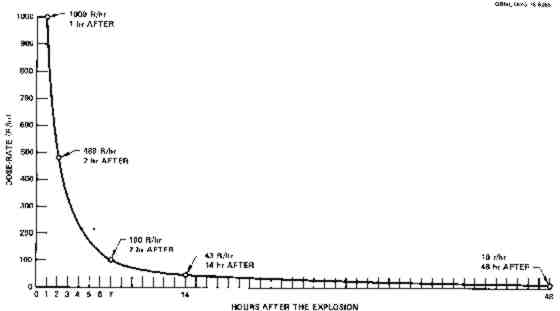
Радиоактивность осадков после атомного взрыва хорошо описывается гиперболическим законом - правило 7-10 (src) говорит что радиоактивность убывает в 10 раз за промежуток времени в 7 раз больше предыдущего. Т.е. если у нас 1000 Р/ч через час после взрыва, то через 7 часов будет 100 Р/ч, через пару суток (49 ч) - 10 Р/ч.

Нетрудно припомнить что одиночный изотоп разлагается по экспоненциальному закону. Я никогда не видел объяснения этого правила, при этом его простота намекает на простой механизм - экспонента описывает систему с одиночной обратной связью, гипербола с двойной.



Попробуем промоделировать распад. Возьмем по грамму полусотни изотопов со логарифмически равномерным временем распада (первый изотоп - 1 секунда, второй - две с, третий - четыре с, и т.д.) от 1 секунды до 3 лет и оценим функцию радиоактивности за пару недель. Гипербола лишь немного лучше экспоненты. :(

А теперь дропнем первый десяток точек и теперь гипербола подходит почти идеально - квадрат ошибки в десять миллиардов раз меньше чем для экспоненты. Распределение изотопов по весу станет таким:



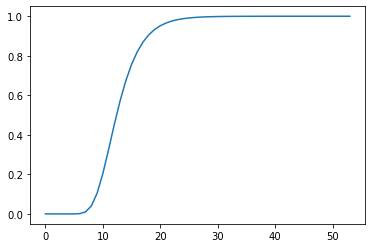
причем сигмоида будет двигаться вправо. Характерное время распада смеси прямо пропорционально пройденному времени - это и дает вторую обратную связь. (вторая отридцательная обратная связь замедляет распад, по сравнению с экспонентой)

Если мы учтем что продукты распада также радиоактивны это не сильно изменит ситуацию - гипербола будет работать даже если 90% осколков радиоактивны. Аналогично гипербола неплохо справится с небольшими нелинейностями и даже с равномерным случайным логарифмическим распределением изотопов по весу.

Полагаю, можно вывести красивое решение дифференциального уравнения, которое даст именно гиперболу, но мой дифференциальный кунг-фу недостаточно силен для того чтобы делать это в рамках развлечения.

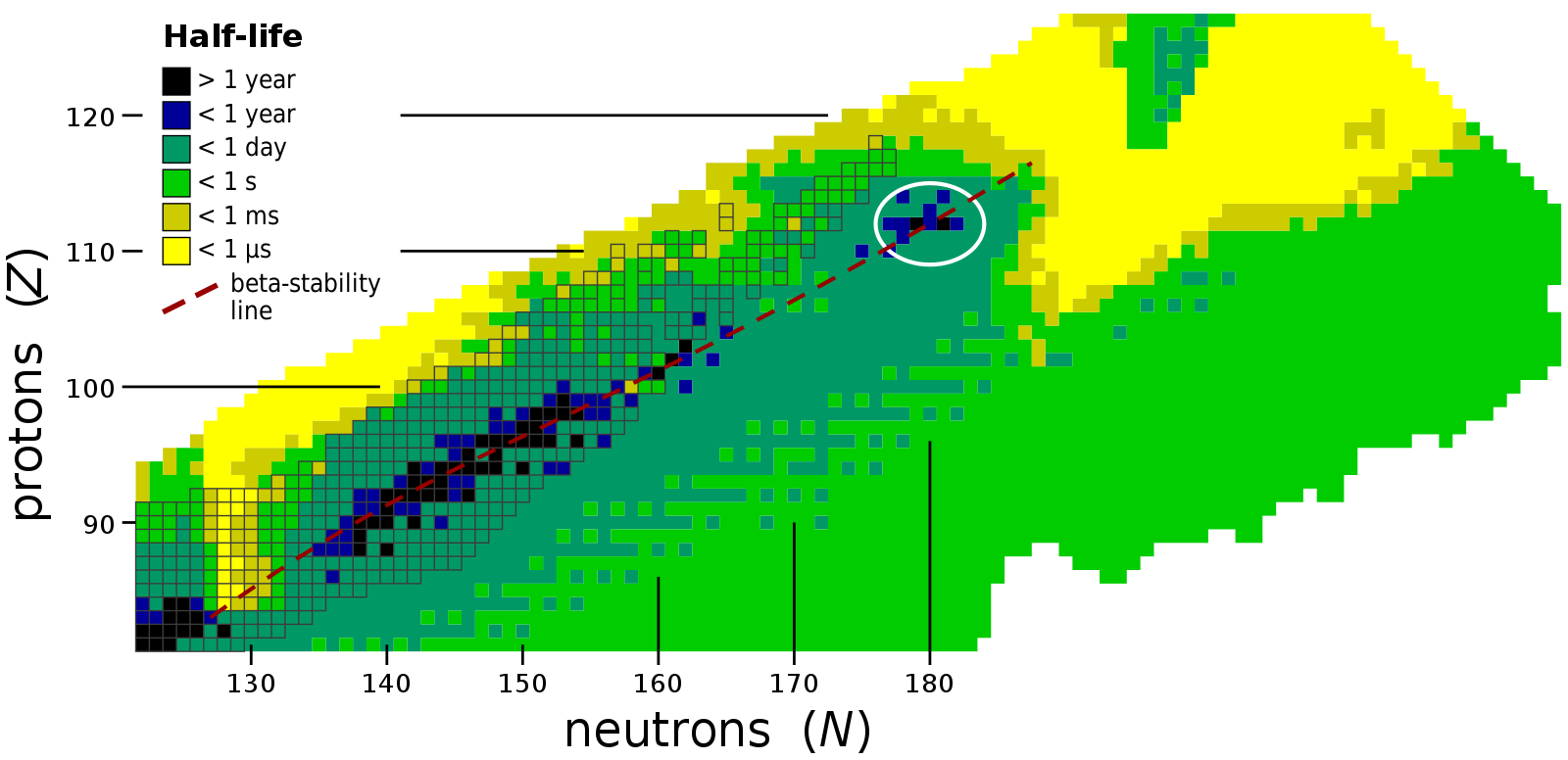
Если взять тысячу с лишним изотопов с известными временами распада мы получим график вроде



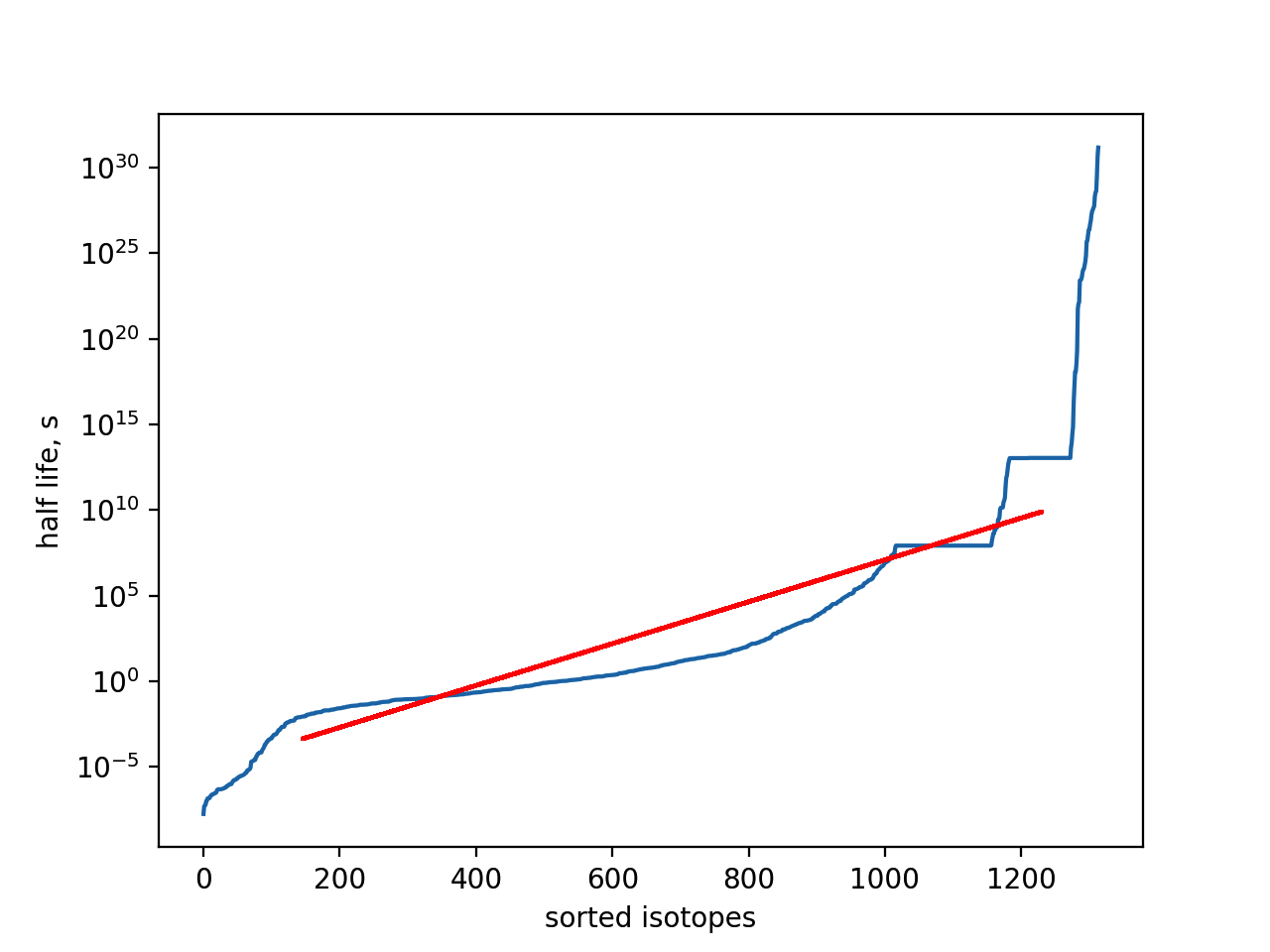
очевидно эта линейность и порождает гиперболу (строго говоря график говорит о всех изотопах и не очевидно почему равномерно распределены продукты распада).

Comments

[vashu11.livejournal.com]

код https://github.com/vashu1/data_snippets/blob/master/fallout_7_10_rule/fallout_7_10_rule.ipynb

[komo78.livejournal.com]

Ну насколько знаю , напуганные радиацией и всякой фантастикой уже с 60-х начали пилить "чистое" ЯО ,.
И сейчас количество несработавшего материала минимально + выхлоп в основном в виде изотопов краткоживущих и вторичной радиации вызванных потоком нейтронов в окружающей среде .
Так что сейчас ЯО "экологично" и того ужаса что у Нэвила Шюта "На берегу" когда из за применения грязных бомб с кобальтовой оболочкой ждать не приходится. Так что у южного полушария неплохие шансы выжить есть .

[vashu11.livejournal.com]

Скорость распада экспоненциально зависит от энергии связи. По видимому энергия связи в интересующем нас диапазоне распространена относительно равномерно

https://en.wikipedia.org/wiki/Spontaneous_fission
Spontaneous fission half-life of various nuclides depending on their Z2/A ratio.

Beta-decay half-lives calculated on the gross theory
https://www.sciencedirect.com/science/article/abs/pii/0092640X73900156

https://en.wikipedia.org/wiki/Nuclear_fission_product
The portion of the total radiation dose (in air) contributed by each isotope versus time after the Chernobyl disaster,

http://nuclphys.sinp.msu.ru/radioactivity/ract07.htm
Самопроизвольное деление ядер с Z2/A < 49, для которых высота барьера H не равна нулю, с точки зрения классической физики невозможно. Однако в квантовой механике такое деление возможно за счет туннельного эффекта – прохождения осколков деления через потенциальный барьер. Оно носит название спонтанного деления. Вероятность спонтанного деления растет с увеличением параметра деления Z2/A, т. е. с уменьшением высоты барьера деления.

Характерной особенностью деления является то, что осколки, как правило, имеют различные массы.
http://nuclphys.sinp.msu.ru/fission/images/fig08f.gif
Рис. 7.4. Массовое распределение осколков деления 235U тепловыми нейтронами.

Отношение числа нейтронов к числу протонов в ядре 235U N/Z = 1.55, в то время как у стабильных изотопов, имеющих массовое число, близкое к массовому числу осколков, это отношение 1.25 − 1.45. Следовательно, осколки деления оказываются сильно перегружеными нейтронами и должны быть
β- радиоактивны. Поэтому, осколки деления испытывают последовательные β--распады, причем заряд первичного осколка может изменяться на 4 − 6 единиц.

http://nuclphys.sinp.msu.ru/radioactivity/ract10.htm
Рис. 10.2. Зависимость логарифма парциального периода кластерного распада от логарифма проницаемости кулоновского потенциального барьера

https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%8F%D0%B4%D1%80%D0%B0#%D0%A1%D0%BF%D0%BE%D0%BD%D1%82%D0%B0%D0%BD%D0%BD%D0%BE%D0%B5_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5
Массовое распределение осколков деления тепловыми нейтронами для некоторых изотопов

https://en.wikipedia.org/wiki/Fission_product_yield
Yields at 100,1,2,3 years after fission,

https://bigenc.ru/physics/text/1945700
Для не­ко­то­рых спон­тан­но де­ля­щих­ся ядер (U, Pu) ха­рак­тер­но асим­мет­рич­ное де­ле­ние, но по ме­ре уве­ли­че­ния A де­ле­ние при­бли­жа­ет­ся к сим­мет­рич­но­му. Наи­бо­лее от­чёт­ли­во это про­яв­ля­ет­ся у 258Fm. Кла­стер­ная ра­дио­ак­тив­ность, ко­гда из яд­ра вы­ле­та­ют лёг­кие яд­ра от 14С до 34Si, так­же мо­жет рас­смат­ри­вать­ся как очень асим­мет­рич­ное де­ле­ние на два ос­кол­ка.

https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%BA%D0%BE%D0%BD_%D0%93%D0%B5%D0%B9%D0%B3%D0%B5%D1%80%D0%B0_%E2%80%94_%D0%9D%D0%B5%D1%82%D1%82%D0%BE%D0%BB%D0%BB%D0%B0
Закон Гейгера — Неттолла — закон, описывающий функциональную связь между энергией альфа-частицы и периодом полураспада радиоактивного ядра.

[vashu11.livejournal.com]

(https://physics.stackexchange.com/questions/743652/isotopes-half-lives-distribution-is-it-log-uniform)

radioactivity - Isotopes half-lives distribution - is it log-uniform? - Physics Stack Exchange

physics.stackexchange.com